Planes#

All Lentil planes are derived from the Plane class. This base class defines the interface to represent any discretely sampled plane in an optical model. Planes typically have some influence on the propagation of a wavefront though this is not strictly required and models may use dummy or reference planes as needed.

Lentil provides several general planes that are the building blocks for most optical models:

  • The Plane base class provides the core logic for representing and working with discretely sampled planes in an optical model.

  • The Pupil plane provides a convenient way to represent a pupil plane in an optical system. There is nothing particularly special about pupil planes, they merely provide a convenient location (mathematically-speaking) to enforce limiting apertures or stops and include optical aberrations. More detailed discussion of pupil planes is available in [1].

  • The Image plane provides a location where the image formed by an optical system may be manipulated or viewed.

In addition, several “utility” planes are provided. These planes do not represent physical components of an optical system, but are used to implement commonly encountered optical effects:

  • The Tilt plane is used to represent wavefront tilt in terms of radians of x and y tilt.

  • The Rotate plane rotates a wavefront by an arbitrary angle.

  • The Flip plane flips a wavefront about its x, y, or both x and y axes.

Plane#

Lentil’s Plane class represents a discretely sampled plane in an optical model. Planes have attributes for representing the sampled complex amplitude of the plane as well as additional metadata that may influence how a propagating wavefront interacts with the plane. A plane is defined by the following parameters:

  • amplitude - Defines the relative electric field amplitude transmission through the plane

  • opd - Defines the optical path difference that a wavefront experiences when propagating through the plane

  • mask - Defines the binary mask over which the plane data is valid. If mask is 2-dimensional, the plane is assumed to be monolithic. If mask is 3-dimensional, the plane is assumed to be segmented with the individual segment masks inserted along the first dimension. If mask is not provided, it is automatically created as needed from the nonzero values in amplitude.

../../_images/segmask.png

  • pixelscale - Defines the physical sampling of the above attributes. A simple example of how to calculate the pixelscale for a discretely sampled circular aperture is given below: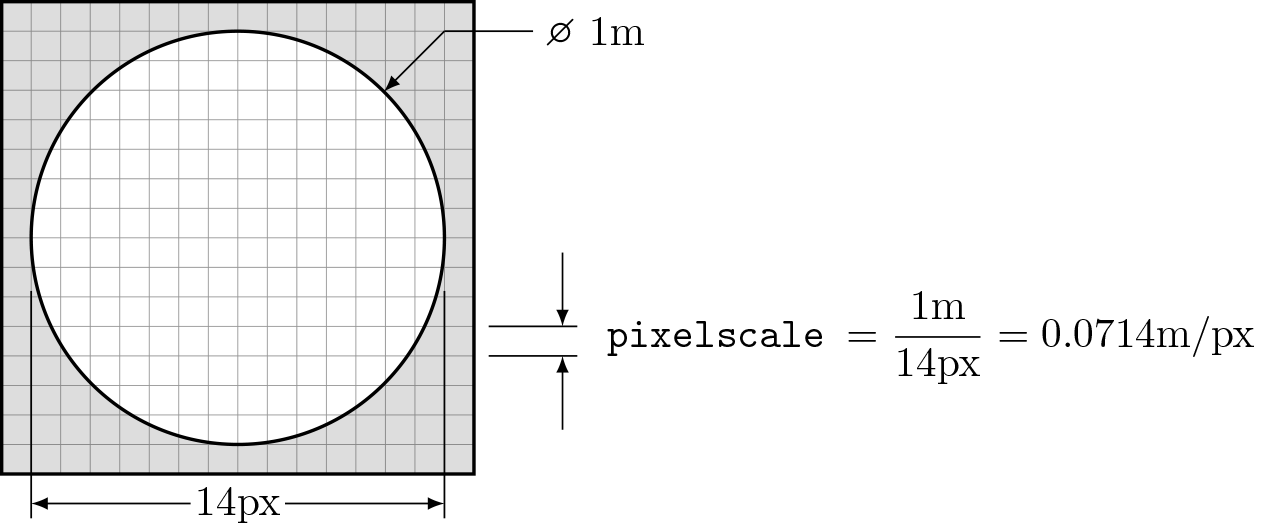

    ../../_images/pixelscale.png

Note

All Plane attributes have sensible default values that have no effect on propagations when not specified.

Create a new Plane with

>>> p = lentil.Plane(amplitude=lentil.circle((256,256), 120))
>>> plt.imshow(p.amplitude, cmap='gray')
../../_images/planes-1.png

Once a Plane is defined, its attributes can be modified at any time:

>>> p = lentil.Plane(amplitude=lentil.circle((256,256), 120))
>>> p.opd = 2e-6 * lentil.zernike(p.mask, index=4)
>>> plt.imshow(p.opd)
../../_images/planes-2.png

Resampling or rescaling a Plane#

It is possible to resample a plane using either the resample() or rescale() methods. Both methods use intrepolation to resample the amplitude, opd, and mask attributes and readjust the pixelscale attribute as necessary.

ptype#

A plane’s type (ptype) defines how it interacts with a Wavefront. When a wavefront interacts with a plane, it inherits the plane’s ptype. Plane type is set automatically and unexpected behavior may occur if it is changed.

Lentil planes support the following ptypes:

ptype

Planes with this type

none

Plane

pupil

Pupil

image

Image

tilt

Tilt, DispersiveTilt

transform

Rotate, Flip

The rules defining when a wavefront is allowed to interact with a plane based on ptype are described here.

Pupil#

Lentil’s Pupil class provides a convenient way to represent a generalized pupil function. Pupil planes behave exactly like Plane objects but introduce an implied spherical phase term defined by the focal_length attribute. The spherical phase term is opaque to the user but is given by

\[\frac{1}{2f} \left(x^2 + y^2\right)\]

where \(f\) is the focal length and \(x\) and \(y\) are pupil plane coordinates.

A pupil is defined by the following required parameters:

  • focal_length - The effective focal length (in meters) represented by the pupil

  • pixelscale - Defines the physical sampling of each pixel in the discretely sampled attributes described below

Discreetly sampled pupil attributes can also be specified:

  • amplitude - Defines the relative electric field amplitude transmission through the pupil

  • opd - Defines the optical path difference that a wavefront experiences when propagating through the pupil.

  • mask - Defines the binary mask over which the pupil data is valid. If mask is 2-dimensional, the pupil is assumed to be monolithic. If mask is 3-dimensional, the pupil is assumed to be segmented with the segment masks allocated along the first dimension. If mask is not provided, it is automatically created as needed from the nonzero values in amplitude.

Note

All optional Pupil attributes have sensible default values that have no effect on propagations when not defined.

Create a pupil with:

>>> p = lentil.Pupil(focal_length=10, pixelscale=1/100, amplitude=1, opd=0)

Image#

Lentil’s Image plane is used to either manipulate or view a wavefront at an image plane in an optical system. An image plane does not have any required parameters although any of the following can be specified:

  • pixelscale - Defines the physical sampling of each pixel in the image plane. If not provided, the sampling will be automatically selected to ensure the results are at least Nyquist sampled.

  • shape - Defines the shape of the image plane. If not provided, the image plane will grow as necessary to capture all data.

  • amplitude - Definers the relative electric field amplitude transmission through the image plane.

  • opd - Defines the optical path difference that a wavefront experiences when propagating through the image plane.

Tilt#

The Tilt plane provides a mechanism for directly specifying wavefront tilt outside of the context of a discretely sampled Plane object. Tilt is most useful for representing global tilt in an optical system (for example, due to a pointing error).

Given the following Pupil plane:

>>> pupil = lentil.Pupil(amplitude=lentil.circle((256, 256), 120),
...                      focal_length=10, pixelscale=1/250)
>>> w = lentil.Wavefront(650e-9)
>>> w *= pupil
>>> w = lentil.propagate_dft(w, pixelscale=5e-6, shape=(64,64), oversample=2)
>>> plt.imshow(w.intensity, cmap='inferno')
../../_images/planes-3.png

It is simple to see the effect of introducing a tilted wavefront into the system:

>>> pupil = lentil.Pupil(amplitude=lentil.circle((256, 256), 120),
...                      focal_length=10, pixelscale=1/250)
>>> tilt = lentil.Tilt(x=10e-6, y=-5e-6)
>>> w = lentil.Wavefront(650e-9)
>>> w *= pupil
>>> w *= tilt
>>> w = lentil.propagate_dft(w, pixelscale=5e-6, shape=(64,64), oversample=2)
>>> plt.imshow(w.intensity, origin='lower', cmap='inferno')
../../_images/planes-4.png

Note

Notice the use of origin='lower' in the plot above. For an explanation, see the note here.

Dispersive planes#

DispersiveTilt#

Grism#

Warning

Grism is deprecated and will be removed in a future version. Use DispersiveTilt instead.

A grism is a combination of a diffraction grating and a prism that creates a dispersed spectrum normal to the optical axis. This is in contrast to a single grating or prism, which creates a dispersed spectrum at some angle that deviates from the optical axis. Grisms are most commonly used to create dispersed spectra for slitless spectroscopy or to create interference fringes for dispersed fringe sensing.

Lentil’s Grism plane provides a straightforward mechanism for efficiently modeling a grism.

Active optics and deformable mirrors#

Active optics and deformable mirrors are easily represented by defining an OPD that depends on some parameterized state. Because there is no standard architecture for these types of optical elements, Lentil does not provide a concrete implementation. Instead, a custom subclass of either Plane or Pupil should be defined. The exact implementation details will vary by application, but a simple example of a tip-tilt mirror where the plane’s OPD is computed dynamically based on the state x is provided below.

import lentil
import numpy as np

class TipTiltMirror(lentil.Plane):

    def __init__(self):
        self.amplitude = lentil.circle((256,256),120)

        self.x = np.zeros(2)

        # Note that we set normalize=False so that each mode spans [-1, 1]
        # and then multiply by 0.5 so that each mode has peak-valley = 1
        self._infl_fn = 0.5 * lentil.zernike_basis(mask=self.amplitude,
                                                   modes=[2,3],
                                                   normalize=False)

    @property
    def opd(self):
        return np.einsum('ijk,i->jk', self._infl_fn, self.x)

>>> tt = TipTiltMirror()
>>> tt.x = [1e-6, 3e-6]
>>> plt.imshow(tt.opd)
>>> plt.colorbar()
../../_images/planes-5.png