Discrete Fourier Transform#
The discrete Fourier transform (DFT) is at the heart of Lentil’s diffraction modeling capability. In addition to FFT-based propagation routines, Lentil includes propagation routines using the matrix triple product formulation of the DFT described in [1]. The code below validates Lentil’s DFT implementation against Numpy’s FFT.
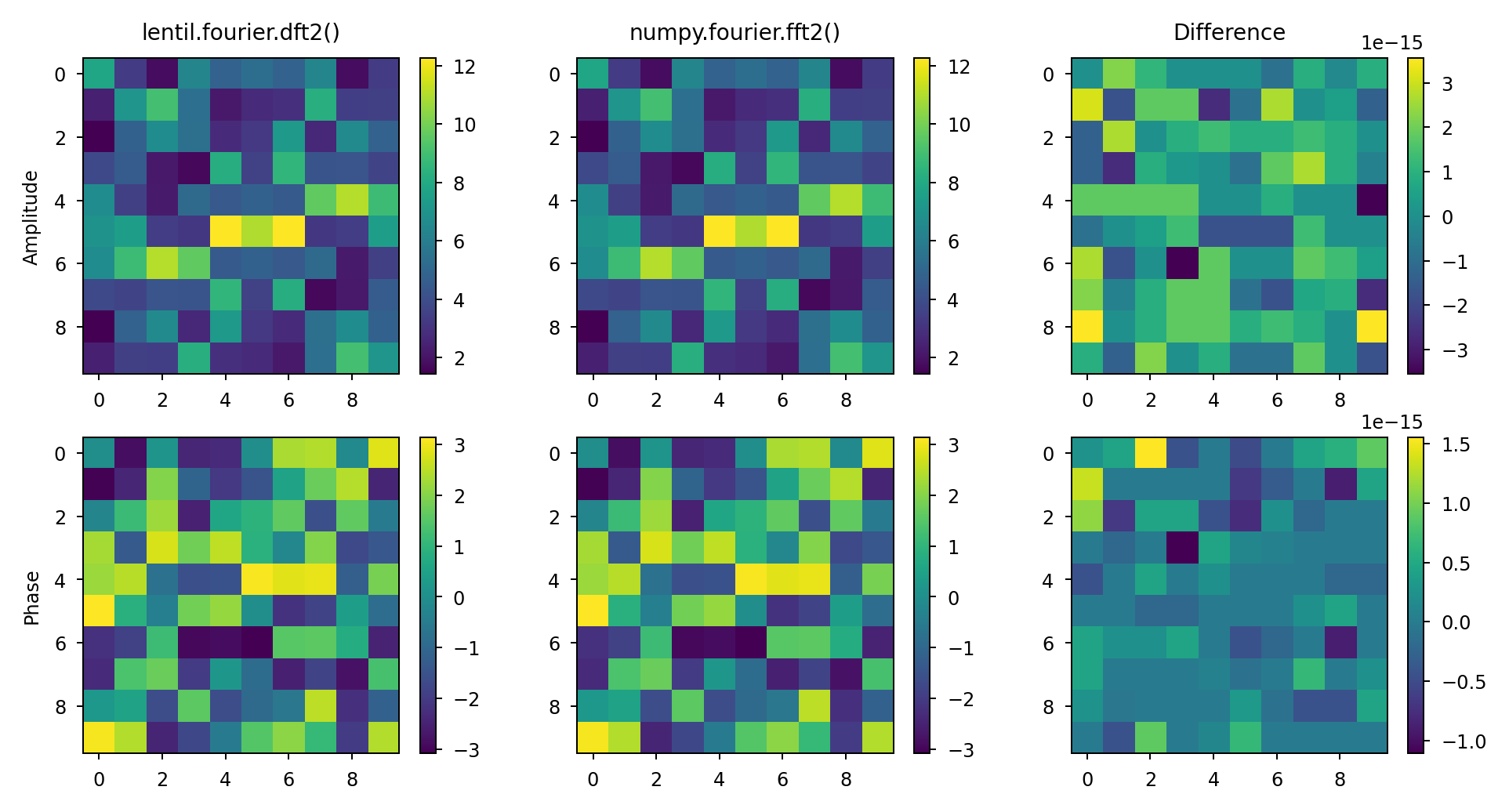
lentil.fourier.dft2() == numpy.fourier.fft2() for even sized input#
n = 10
f = np.random.uniform(low=-1, high=1, size=(n, n))
F_dft = lentil.fourier.dft2(f, 1/n, unitary=False)
F_fft = np.fft.fftshift(np.fft.fft2(np.fft.ifftshift(f)))
fig, ax = plt.subplots(nrows=2, ncols=3, figsize=(8,4))
abs_dft = ax[0,0].imshow(np.abs(F_dft))
ax[0,0].set_ylabel('Amplitude')
ax[0,0].set_title('lentil.fourier.dft2()')
plt.colorbar(abs_dft, ax=ax[0,0])
abs_fft = ax[0,1].imshow(np.abs(F_fft))
ax[0,1].set_title('numpy.fourier.fft2()')
plt.colorbar(abs_fft, ax=ax[0,1])
abs_diff = ax[0,2].imshow(np.abs(F_dft) - np.abs(F_fft))
ax[0,2].set_title('Difference')
plt.colorbar(abs_diff, ax=ax[0,2])
angle_dft = ax[1,0].imshow(np.angle(F_dft))
ax[1,0].set_ylabel('Phase')
plt.colorbar(angle_dft, ax=ax[1,0])
angle_fft = ax[1,1].imshow(np.angle(F_fft))
plt.colorbar(angle_fft, ax=ax[1,1])
angle_diff = ax[1,2].imshow(np.angle(F_dft) - np.angle(F_fft))
plt.colorbar(angle_diff, ax=ax[1,2])
assert np.allclose(F_dft, F_fft)
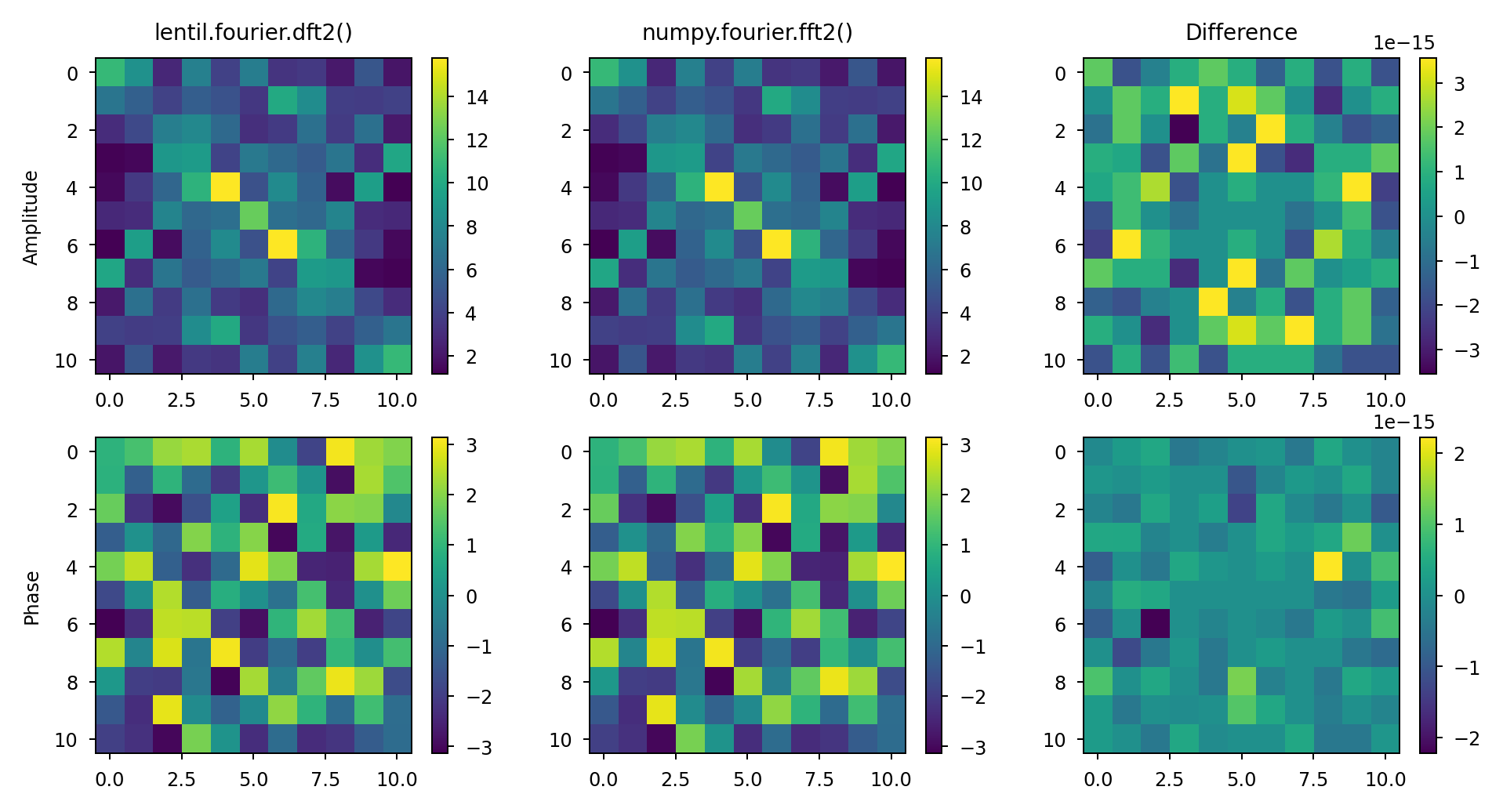
lentil.fourier.dft2() == numpy.fourier.fft2() for odd sized input#
n = 11
f = np.random.uniform(low=-1, high=1, size=(n, n))
F_dft = lentil.fourier.dft2(f, 1/n, unitary=False)
F_fft = np.fft.fftshift(np.fft.fft2(np.fft.ifftshift(f)))
fig, ax = plt.subplots(nrows=2, ncols=3, figsize=(8,4))
abs_dft = ax[0,0].imshow(np.abs(F_dft))
ax[0,0].set_ylabel('Amplitude')
ax[0,0].set_title('lentil.fourier.dft2()')
plt.colorbar(abs_dft, ax=ax[0,0])
abs_fft = ax[0,1].imshow(np.abs(F_fft))
ax[0,1].set_title('numpy.fourier.fft2()')
plt.colorbar(abs_fft, ax=ax[0,1])
abs_diff = ax[0,2].imshow(np.abs(F_dft) - np.abs(F_fft))
ax[0,2].set_title('Difference')
plt.colorbar(abs_diff, ax=ax[0,2])
angle_dft = ax[1,0].imshow(np.angle(F_dft))
ax[1,0].set_ylabel('Phase')
plt.colorbar(angle_dft, ax=ax[1,0])
angle_fft = ax[1,1].imshow(np.angle(F_fft))
plt.colorbar(angle_fft, ax=ax[1,1])
angle_diff = ax[1,2].imshow(np.angle(F_dft) - np.angle(F_fft))
plt.colorbar(angle_diff, ax=ax[1,2])
assert np.allclose(F_dft, F_fft)